Finite Automata For lexical analysis: Specification Regular - PDF document

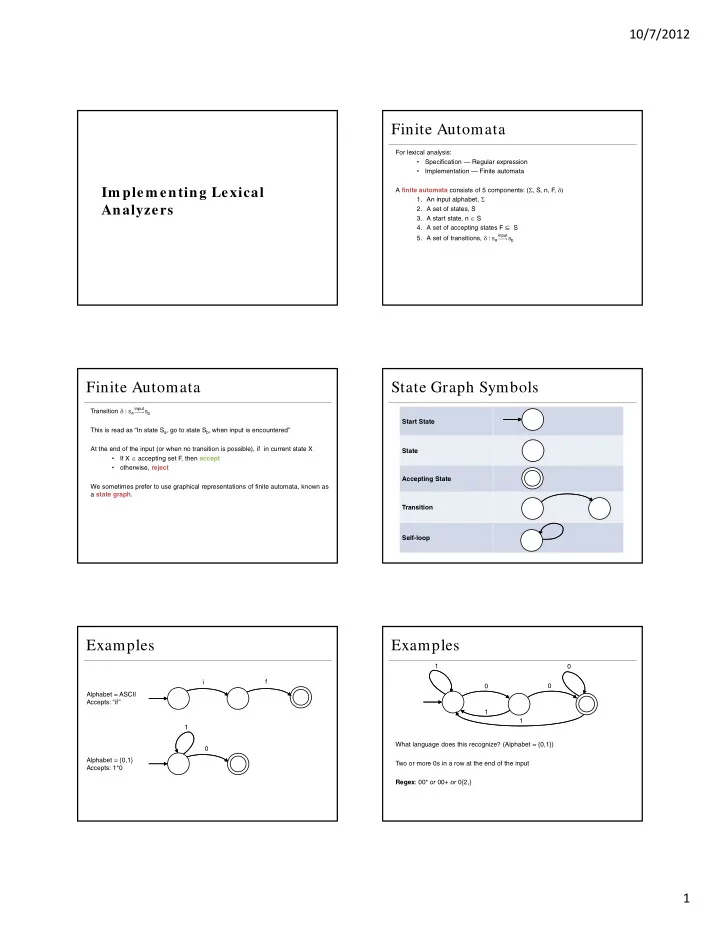
10/7/2012 Finite Automata For lexical analysis: • Specification — Regular expression • Implementation — Finite automata A finite automata consists of 5 components: (  , S, n, F ,  Im plem enting Lexical 1. An input alphabet,  Analyzers 2. A set of states, S 3. A start state, n  S 4. A set of accepting states F ⊆ S 5. A set of transitions,  : Sa input Sb Finite Automata State Graph Symbols Transition  : Sa input Sb Start State This is read as “In state S a , go to state S b , when input is encountered” At the end of the input (or when no transition is possible), if in current state X State If X  accepting set F • , then accept • otherwise, reject Accepting State We sometimes prefer to use graphical representations of finite automata, known as a state graph . Transition Self-loop Examples Examples 1 0 f i 0 0 Alphabet = ASCII Accepts: “if” 1 1 1 What language does this recognize? (Alphabet = {0,1}) 0 Alphabet = {0,1} Two or more 0s in a row at the end of the input Accepts: 1*0 Regex : 00* or 00+ or 0{2,} 1

10/7/2012 Table Implementation Table Implementation 0 0 0 0 Input T T 0 1 S T U State S S 1 1 0 0 T T U U T X U U 1 1 Table-driven Code Epsilon Transitions FSA() { state = ‘S’;  while (!done) { ch = fetch_input(); A B state = Table[state][ch]; if (state == ‘X’) { System.err.println(“error”); } Another kind of transition:  - transition } • Machine can move from state A to state B without reading any input if (state  F){ System.out.println(“accept”); } else { System.out.println(“reject”); } } DFA & NFAs Converting REs to NFAs Deterministic Finite Automata (DFA): Thompson’s Algorithm • One transition per input per state REs can be converted to NFAs. Atomic REs are straightforward. • No  -moves  Non-deterministic Finite Automata (NFA): Epsilon transitions: • Can have multiple transitions for one input in a given state • Can have  -moves Finite automata have finite memory a • Need only to encode the current state Single characters: 2

10/7/2012 Converting REs to NFAs Converting REs to NFAs Kleene Closure: * Alternation: N 1   N 1 N 1 | N 2      N 2 N 1  Concatenation: N 1 N 2 N 1 N 2 Example Example Convert (a|b)*ab to an NFA Convert (a|b)*ab to an NFA Step 1: a a Example Example Convert (a|b)*ab to an NFA Convert (a|b)*ab to an NFA Step 2: b Step 3: (a|b) a a     b b 3

10/7/2012 Example Example Convert (a|b)*ab to an NFA Convert (a|b)*ab to an NFA Step 4: (a|b)* Step 5: (a|b)*a   a a         a     b b   Example Executing Finite Automata Convert (a|b)*ab to an NFA A DFA can take only one path through the state graph • Completely determined by input Step 6: (a|b)*ab  A NFA can take multiple paths “simultaneously” • NFAs make  -transitions a •  There may be multiple transitions out of a state for a single input  • Rule : the NFA accepts it if can get into a final state by any path   a b   Which is more powerful, an NFA or a DFA? b  Power of NFAs and DFAs Example Theorem: NFAs and DFAs recognize the same set of languages NFA and DFA that accept (a|b)*ab  Both recognize regular languages. a     a b DFAs are faster to execute because there are no choices to consider.   b  For a given language, the NFA can be simpler than the DFA – a DFA can be exponentially larger. b b a b a a 4

10/7/2012 NFA to DFA Conversion Epsilon-Closure Let edge ( s , c ) be the set of all NFA states reachable by following a single edge with Basic idea: Given a NFA, simulate its execution using a DFA label c from state s . • At step n , the NFA may be in any of multiple possible states For a set of states S,  -closure (S) is the set of states that can be reached from a state in S via  -transitions. The new DFA is constructed as follows: • The states of the DFA correspond to a non-empty subset of states of the NFA ������������ � � ∪ � ������, �� �∈� ’s start state is the set of NFA states reachable through  - • The DFA function  -closure(S) transitions from NFA start state T ← S � repeat • A transition Sa → Sb is added iff S b is the set of NFA states reachable T’ ← T from any state in S a after seeing the input c , also considering  - T � T′ ∪ ⋃ edge�s, ε� �∈�� transitions until T=T’ return T Start State NFA to DFA Conversion Example   a a     2 3 2 3     a b a b 0 1 6 7 8 9 0 1 6 7 8 9     b b 4 5 4 5   ’s start state =  -closure(S 0 ) The NFA ’s start state is S 0 , so the DFA Start state =  -closure(S 0 ) = {0, 1, 2, 4, 7} = A By iteration: We’ll call this collection of states A, and will be a new node in our DFA that is our T 1 = S 0 = {S 0 } DFA start state. T 2 = T 1 ∪  -closure(T 1 ) = {S 0 , S 1 , S 7 } Set Name T 3 = T 2 ∪  -closure(T 2 ) = {S 0 , S 1 , S 2 , S 4 , S 7 } {0, 1, 2, 4, 7} A T 4 = T 3 ∪  -closure(T 3 ) = {S 0 , S 1 , S 2 , S 4 , S 7 } A T 4 = T 3 so we are done. Construct DFA Construct DFA   a a    2 3  2 3     a b a b 0 1 6 7 8 9 0 1 6 7 8 9     b b 4 5 4 5   , considering each state in A, we could go to 5, but we must do the  - We now compute where we can go from A on each input in our alphabet. On an ‘b’ closure. On an ‘a’ , considering each state in A, where might we end up? An a would take us from 2 to 3 and from 7 to 8. But we must consider our ε -transitions as well. C = ε -closure(5) = {1, 2, 4, 5, 6, 7} B = ε -closure(3) ∪ ε -closure(8) = {1, 2, 3, 4, 6, 7 } ∪ {8} Set Name Set Name B B a a {0, 1, 2, 4, 7} A {0, 1, 2, 4, 7} A A A {1, 2, 3, 4, 6, 7 , 8 } B {1, 2, 3, 4, 6, 7 , 8 } B b {1, 2, 4, 5, 6, 7} C C 5

10/7/2012 Construct DFA Construct DFA   a a     2 3 2 3    a  a b b 0 1 6 7 8 9 0 1 6 7 8 9     b b 4 5 4 5   Repeat process for B: Repeat process for C: In B, see an ‘a’ = {1, 2, 3, 4, 6, 7 , 8} = B (Self loop) In C, see an ‘a’ = {1, 2, 3, 4, 6, 7 , 8} = B In B, see a ‘b’ = {1, 2, 4, 5, 6, 7 , 9} = D In C, see a ‘b’ = {1, 2, 4, 5, 6, 7} =C (Self loop) a a b b Set Name Set Name B D B D a a {0, 1, 2, 4, 7} A {0, 1, 2, 4, 7} A A A a {1, 2, 3, 4, 6, 7 , 8 } B {1, 2, 3, 4, 6, 7 , 8 } B b b {1, 2, 4, 5, 6, 7} C {1, 2, 4, 5, 6, 7} C C C {1, 2, 4, 5, 6, 7 , 9} D {1, 2, 4, 5, 6, 7 , 9} D b Construct DFA DFA Final States  A state in the DFA is final if one of the states in the set of NFA states is final. a   2 3   a b a 0 1 6 7 8 9   b 4 5  Repeat process for D: b Set Name B D a In D, see an ‘a’ = {1, 2, 3, 4, 6, 7 , 8} = B {0, 1, 2, 4, 7} A a In D, see a ‘b’ = {1, 2, 4, 5, 6, 7} =C {1, 2, 3, 4, 6, 7 , 8 } B A a b a b {1, 2, 4, 5, 6, 7} C {1, 2, 4, 5, 6, 7 , 9 } D C b Set Name B D a {0, 1, 2, 4, 7} A a b A a b {1, 2, 3, 4, 6, 7 , 8 } B b {1, 2, 4, 5, 6, 7} C C {1, 2, 4, 5, 6, 7 , 9} D b NFA to DFA Remarks Why DFAs? This algorithm does not produce a minimal DFA. Why’d we do all that work? It does however, exclude states that are not reachable from the start state. A DFA can be implemented by a 2D table T: • One dimension is states, the other dimension is input characters This is important because an n-state NFA could have 2 n states as a DFA. � → Sb we have T[S a ,c] = S b • For Sa (Why? Set of all subsets.) DFA execution: The minimization algorithm is left to the graduate course. • If the current state is S a and input is c, then read T[S a ,c] • Update the current state to S b , assuming S b = T[S a ,c] • This is very efficient 6

10/7/2012 Automating Automatons Implementation RE → NFA → DFA → Table-driven Implementation If we have algorithmic ways to convert REs to NFAs and to convert NFAs to faster DFAs, we could have a program where we write our lexical rules using REs and • Specify lexical structure using regular expressions automatically have a table-driven lexer produced. Finite automata • Deterministic Finite Automata (DFAs) NFA to DFA conversion is the heart of automated tools such as lex/flex/JLex/Jflex • Non-deterministic Finite Automata (NFAs) • DFA could be very large Table implementation • In practice, lex-like tools trade off speed for space in the choice of NFA and DFA representations Lexical Specification Manual conversion Set of Table-driven Regular NFA DFA Implementation Expressions Automatic conversion Scanner Automaton Ambiguity Resolution Imagine a rule for C identifiers: letter | digit | _ [a-zA-Z_][a-zA-Z0-9_]* other return IDENTIFIER; And the rule for a keyword such as if: “if” letter | _ digit How do we resolve the fact that if is a keyword and if8 is an identifier? digit other return INT_CONST; Two rules: 1. Longest match – The match with the longest string will be chosen. 2. Rule priority – for two matches of the same length, the first regex will be chosen. I.e., Rule order matters. > = return OP_GE; other return OP_GT; 7