18. Binary Search Trees Special graphs: graphs consist of nodes and - PowerPoint PPT Presentation

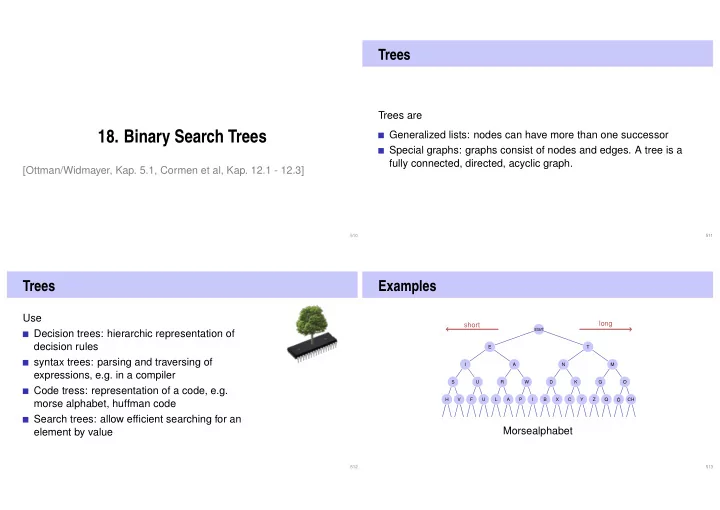
Trees Trees are Generalized lists: nodes can have more than one successor 18. Binary Search Trees Special graphs: graphs consist of nodes and edges. A tree is a fully connected, directed, acyclic graph. [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap. 12.1 - 12.3] 510 511 Trees Examples Use long short start Decision trees: hierarchic representation of decision rules E T syntax trees: parsing and traversing of I A N M expressions, e.g. in a compiler S U R W D K G O Code tress: representation of a code, e.g. H V F U L A P I B X C Y Z Q CH morse alphabet, huffman code Ö Search trees: allow efficient searching for an Morsealphabet element by value 512 513

Examples Nomenclature Wurzel 3 / 5 + 7 . 0 W + parent inner node I E child K / 7 . 0 leaves 3 5 Order of the tree: maximum number of child nodes, here: 3 Expression tree Height of the tree: maximum path length root – leaf (here: 4) 514 515 Binary Trees Recall: Linked List Node in Java ListNode A binary tree is either 1 5 6 null either a leaf, i.e. an empty tree, next (type ListNode ) key (type int ) or an inner leaf with two trees T l (left subtree) and T r (right subtree) as left and right successor. class ListNode { In each node v we store key int key; ListNode next; right left a key v. key and ListNode (int key, ListNode next){ two nodes v. left and v. right to the roots of the left and right this .key = key; subtree. this .next = next; } a leaf is represented by the null -pointer } 516 517

Now: tree nodes in Java Binary search tree A binary search tree is a binary tree that fulfils the search tree SearchNode public class SearchNode { property : key (type int ) 5 int key; // Schluessel Every node v stores a key SearchNode left; // linker Teilbaum Keys in left subtree v.left are smaller than v.key SearchNode right; // rechter Teilbaum Keys in right subtree v.right are greater than v.key 3 8 // Konstruktor: Knoten ohne Nachfolger SearchNode(int k){ 16 key = k; null null null left = right = null; 2 7 18 } } 5 10 17 30 left (type SearchNode ) right (type SearchNode ) null null 2 9 15 99 518 519 Searching Search Tree and Searching in Java public class SearchTree { Input: Binary search tree with root r , key k SearchNode root = null; // Wurzelknoten Output: Node v with v. key = k or null 8 v ← r // Gibt zurueck, ob Knoten mit Schluessel k existiert while v � = null do public boolean contains (int k){ 4 13 if k = v. key then SearchNode n = root; return v while (n != null && n.key != k){ 10 19 else if k < v. key then if (k < n.key) n = n.left; v ← v. left else n = n.right; else 9 } v ← v. right Search (12) → null return n != null; } return null ... // Einfuegen, Loeschen } 520 521

Height of a tree Insertion of a key Insertion of the key k The height h ( T ) of a tree T with root r is given by 8 Search for k If successful search: output 4 13 � if r = null 0 error h ( r ) = otherwise. 1 + max { h ( r. left) , h ( r. right) } 5 10 19 Of no success: insert the key at the leaf reached 9 The worst case search time is determined by the height of the tree. Implementation: devil is in the Insert (5) detail 522 523 Knoten Einf¨ ugen in Java Remove node public boolean add (int k) { if (root == null) {root = new SearchNode(k); return true;} SearchNode t=root; Three cases possible: 8 while (k != t.key) { if (k < t.key) { Node has no children if (t.left == null){ t.left = new SearchNode(k); return true;} 3 13 Node has one child else { t = t.left; } } 5 10 19 Node has two children else { // k > t.key [Leaves do not count here] if (t.right == null){ t.right = new SearchNode(k); return true;} 4 9 else { t = t.right; } } } return false; } 524 525

Remove node Remove node Node has no children Node has one child Simple case: replace node by leaf. Also simple: replace node by single child. 8 8 8 8 3 13 3 13 3 13 5 13 remove (4) remove (3) − → − → 5 10 19 5 10 19 5 10 19 4 10 19 4 9 9 4 9 9 526 527 Remove node By symmetry... Node v has two children The following observation helps: the Node v has two children 8 8 smallest key in the right subtree v.right Also possible: replace v by its symmetric 3 13 (the symmetric successor of v ) 3 13 predecessor. is smaller than all keys in v.right 5 10 19 5 10 19 is greater than all keys in v.left Implementation: devil is in the detail! 4 9 and cannot have a left child. 4 9 Solution: replace v by its symmetric suc- cessor. 528 529

Algorithm SymmetricSuccessor( v ) SymmetricDesc in Java public SearchNode symmetricDesc(SearchNode node) { if (node.left == null) { return node.right; } if (node.right == null) { return node.left; } Input: Node v of a binary search tree. SearchNode n = node.right; // cannot be null Output: Symmetric successor of v SearchNode parent = null; w ← v. right while (n.left != null) { parent = n; n = n.left; } x ← w. left if (parent != null){ while x � = null do This algorithm returns the symmetric parent.left = n.right; w ← x descendent. But it does even more: it n.right = node.right; x ← x. left handles also all cases with one or no } // else n == node.right return w descendent. And it replaces the sym- n.left = node.left; metric descendent by its successor. return n; } 530 531 Knoten L¨ oschen in Java Traversal possibilities public boolean remove (int k) { SearchNode n = root; preorder: v , then T left ( v ) , then if (n != null && n.key == k) { T right ( v ) . root = SymmetricDesc(root); return true; 8 8, 3, 5, 4, 13, 10, 9, 19 } while (n != null) { 3 13 postorder: T left ( v ) , then T right ( v ) , then if (n.left != null && k == n.left.key) { v . n.left = SymmetricDesc(n.left); return true; 5 10 19 4, 5, 3, 9, 10, 19, 13, 8 } else if (n.right != null && k == n.right.key) { n.right = SymmetricDesc(n.right); return true; inorder: T left ( v ) , then v , then T right ( v ) . 4 9 } else if (k < n.key) { n = n.left; 3, 4, 5, 8, 9, 10, 13, 19 } else { n = n.right; } } return false; } 532 533

Degenerated search trees Efficiency Considerations 4 19 Obviously the runtime of the algorithms search, insert and delete 5 13 depend in the worst case on the heigh of the tree. 9 8 10 Degenerated trees are in the worst case thus not better than a linked list 5 13 9 9 Balanced trees make sure (e.g. with rotations ) during insertion or 10 8 4 8 10 19 deletion that the tree stays balanced and provide certain guarantees Insert 9,5,13,4,8,10,19 13 5 for the algorithms. ideally balanced 19 4 The data structures TreeSet and TreeMap in Java are implemented Insert 4,5,8,9,10,13,19 Insert 19,13,10,9,8,5,4 with balanced trees (so called Red-Black-Trees). linear list linear list 534 535 [Max-]Heap 9 Binary tree with the following prop- Wurzel erties 1 complete up to the lowest 22 level parent 19. Heaps 20 18 2 Gaps (if any) of the tree in the last level to the right child 16 12 15 17 3 Heap-Condition: [Ottman/Widmayer, Kap. 2.3, Cormen et al, Kap. 6] Max-(Min-)Heap: key of a 3 2 8 11 14 child smaller (greater) thant leaves that of the parent node 9 Heap(data structure), not: as in “heap and stack” (memory allocation) 536 537

Heap as Array Heap in Java public class Heap { Tree → Array: double[] A;// will need to grow 22 children ( i ) = { 2 i + 1 , 2 i + 2 } int sz; [0] // Heap initialized with 16 elements parent ( i ) = ⌊ ( i − 1) / 2 ⌋ 20 18 Heap () { [1] [2] A = new double[16]; sz = 0; Vater 16 12 15 17 } [3] [4] [5] [6] // binary growth of the array 22 20 18 16 12 15 17 3 2 8 11 14 3 2 8 11 14 void grow(){ ... } 0 1 2 3 4 5 6 7 8 9 10 11 [7] [8] [9] [10] [11] // insert element in the heap Kinder public void add(double value){...} Depends on the starting index 10 // extract and return first (maximal) element public double remove() {...} } 10 For array that start at 1 : { 2 i + 1 , 2 i + 2 } → { 2 i, 2 i + 1 } , ⌊ ( i − 1) / 2 ⌋ → ⌊ i/ 2 ⌋ 538 539 Algorithm Sift-Up( A, m ) Insert 22 Input : Array A with at least m + 1 and Max-Heap-Structure on 20 18 A [0 , . . . , m − 1] Output : Array A with Max-Heap-Structure on A [0 , . . . , m ] . 16 12 15 17 v ← A [ m ] // value Insert new element at the first free c ← m // current position position. Potentially violates the heap 3 8 2 11 14 p ← ⌊ ( c − 1) / 2 ⌋ // parent node property. while c > 0 and v > A [ p ] do 22 A [ c ] ← A [ p ] // Value parent node → current node Reestablish heap property: climb c ← p // parent node → current node 20 21 successively p ← ⌊ ( c − 1) / 2 ⌋ 16 12 18 17 A [ c ] ← v // value → current node 3 2 8 11 14 15 540 541