Quicksort Proposed by C.A.R. Hoare in 1962. Divide-and-conquer - PowerPoint PPT Presentation

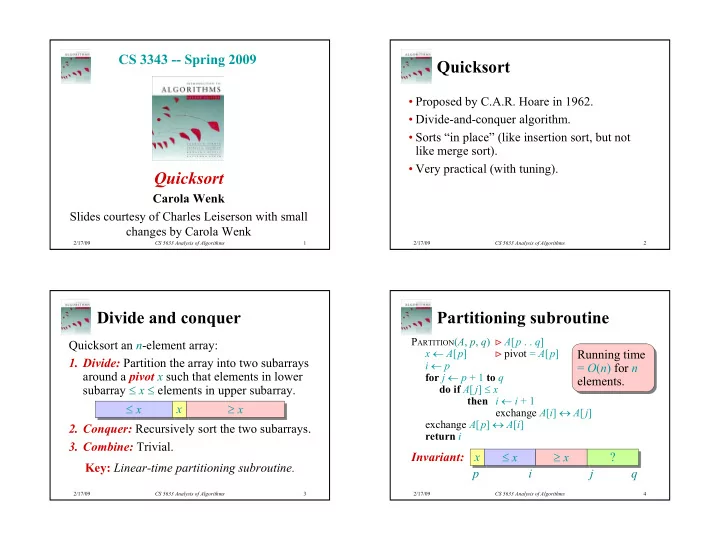
CS 3343 -- Spring 2009 Quicksort • Proposed by C.A.R. Hoare in 1962. • Divide-and-conquer algorithm. • Sorts “in place” (like insertion sort, but not like merge sort). • Very practical (with tuning). Quicksort Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk 2/17/09 CS 5633 Analysis of Algorithms 1 2/17/09 CS 5633 Analysis of Algorithms 2 Divide and conquer Partitioning subroutine P ARTITION ( A , p , q ) ⊳ A [ p . . q ] Quicksort an n -element array: ⊳ pivot = A [ p ] x ← A [ p ] Running time Running time 1. Divide: Partition the array into two subarrays i ← p = O ( n ) for n = O ( n ) for n around a pivot x such that elements in lower for j ← p + 1 to q elements. elements. subarray ≤ x ≤ elements in upper subarray. do if A [ j ] ≤ x then i ← i + 1 ≤ x ≥ x x ≤ x ≥ x x exchange A [ i ] ↔ A [ j ] exchange A [ p ] ↔ A [ i ] 2. Conquer: Recursively sort the two subarrays. return i 3. Combine: Trivial. ≤ x ≥ x Invariant: x ? ≤ x ≥ x x ? Key: Linear-time partitioning subroutine. p i j q 2/17/09 CS 5633 Analysis of Algorithms 3 2/17/09 CS 5633 Analysis of Algorithms 4 1

Example of partitioning Example of partitioning 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 i j i j 2/17/09 CS 5633 Analysis of Algorithms 5 2/17/09 CS 5633 Analysis of Algorithms 6 Example of partitioning Example of partitioning 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 i j 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 i j 2/17/09 CS 5633 Analysis of Algorithms 7 2/17/09 CS 5633 Analysis of Algorithms 8 2

Example of partitioning Example of partitioning 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 i j i j 2/17/09 CS 5633 Analysis of Algorithms 9 2/17/09 CS 5633 Analysis of Algorithms 10 Example of partitioning Example of partitioning 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 3 10 8 13 2 11 6 5 3 10 8 13 2 11 6 5 3 10 8 13 2 11 6 5 3 10 8 13 2 11 i j i j 2/17/09 CS 5633 Analysis of Algorithms 11 2/17/09 CS 5633 Analysis of Algorithms 12 3

Example of partitioning Example of partitioning 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 3 10 8 13 2 11 6 5 3 10 8 13 2 11 6 5 3 10 8 13 2 11 6 5 3 10 8 13 2 11 6 5 3 2 8 13 10 11 6 5 3 2 8 13 10 11 6 5 3 2 8 13 10 11 6 5 3 2 8 13 10 11 i j i j 2/17/09 CS 5633 Analysis of Algorithms 13 2/17/09 CS 5633 Analysis of Algorithms 14 Example of partitioning Example of partitioning 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 10 13 5 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 13 10 8 3 2 11 6 5 3 10 8 13 2 11 6 5 3 10 8 13 2 11 6 5 3 10 8 13 2 11 6 5 3 10 8 13 2 11 6 5 3 2 8 13 10 11 6 5 3 2 8 13 10 11 6 5 3 2 8 13 10 11 6 5 3 2 8 13 10 11 i j 2 5 3 6 8 13 10 11 2 5 3 6 8 13 10 11 i 2/17/09 CS 5633 Analysis of Algorithms 15 2/17/09 CS 5633 Analysis of Algorithms 16 4

Pseudocode for quicksort Analysis of quicksort Q UICKSORT ( A , p, r ) • Assume all input elements are distinct. if p < r then q ← P ARTITION ( A , p, r ) • In practice, there are better partitioning algorithms for when duplicate input Q UICKSORT ( A , p, q –1) elements may exist. Q UICKSORT ( A , q+ 1 , r ) • Let T(n) = worst-case running time on an array of n elements. Initial call: Q UICKSORT ( A , 1 , n ) 2/17/09 CS 5633 Analysis of Algorithms 17 2/17/09 CS 5633 Analysis of Algorithms 18 Worst-case of Worst-case recursion tree quicksort T ( n ) = T (0) + T ( n –1) + cn • Input sorted or reverse sorted. • Partition around min or max element. • One side of partition always has no elements. = + − + Θ T ( n ) T ( 0 ) T ( n 1 ) ( n ) = Θ + − + Θ ( 1 ) T ( n 1 ) ( n ) = − + Θ T ( n 1 ) ( n ) = Θ (arithmetic series) ( n 2 ) 2/17/09 CS 5633 Analysis of Algorithms 19 2/17/09 CS 5633 Analysis of Algorithms 20 5

Worst-case recursion tree Worst-case recursion tree T ( n ) = T (0) + T ( n –1) + cn T ( n ) = T (0) + T ( n –1) + cn T ( n ) cn T (0) T ( n –1) 2/17/09 CS 5633 Analysis of Algorithms 21 2/17/09 CS 5633 Analysis of Algorithms 22 Worst-case recursion tree Worst-case recursion tree T ( n ) = T (0) + T ( n –1) + cn T ( n ) = T (0) + T ( n –1) + cn cn cn T (0) c ( n –1) T (0) c ( n –1) T (0) T ( n –2) T (0) c ( n –2) … T (0) Θ (1) 2/17/09 CS 5633 Analysis of Algorithms 23 2/17/09 CS 5633 Analysis of Algorithms 24 6

Worst-case recursion tree Worst-case recursion tree T ( n ) = T (0) + T ( n –1) + cn T ( n ) = T (0) + T ( n –1) + cn  height  ( )  n  ( ) Θ ∑ Θ ∑ cn cn   = Θ   = Θ 2 2 k n k n         T (0) c ( n –1) T (0) c ( n –1) = = k 1 k 1 T (0) c ( n –2) T (0) c ( n –2) height = n height = n … … T (0) T (0) T (0) T (0) 2/17/09 CS 5633 Analysis of Algorithms 25 2/17/09 CS 5633 Analysis of Algorithms 26 Worst-case recursion tree Best-case analysis (For intuition only!) T ( n ) = T (0) + T ( n –1) + cn If we’re lucky, P ARTITION splits the array evenly:   n ( ) Θ ∑ cn   = Θ 2 k n   T ( n ) = 2 T ( n /2) + Θ ( n )   Θ (1) c ( n –1) = k 1 = Θ ( n log n ) (same as merge sort) Θ (1) c ( n –2) height = n T ( n ) = Θ ( n ) + Θ ( n 2 ) 1 : 9 … What if the split is always ? Θ (1) = Θ ( n 2 ) 10 10 ( ) ( ) = + + Θ T ( n ) T n T n ( n ) 1 9 Θ (1) 10 10 What is the solution to this recurrence? 2/17/09 CS 5633 Analysis of Algorithms 27 2/17/09 CS 5633 Analysis of Algorithms 28 7

Analysis of “almost-best” case Analysis of “almost-best” case cn T ( n ) ( ) ( ) T 10 n 1 T 10 n 9 2/17/09 CS 5633 Analysis of Algorithms 29 2/17/09 CS 5633 Analysis of Algorithms 30 Analysis of “almost-best” case Analysis of “almost-best” case cn cn cn cn cn 1 1 9 cn 9 cn cn 10 10 10 10 log 10/9 n ( ) ( ) ( ) ( ) T 100 n T 100 n T 100 n T 100 n cn cn cn cn cn 1 9 9 81 1 9 9 81 100 100 100 100 … … … Θ (1) O ( n ) leaves O ( n ) leaves Θ (1) 2/17/09 CS 5633 Analysis of Algorithms 31 2/17/09 CS 5633 Analysis of Algorithms 32 8

Analysis of “almost-best” case Quicksort Runtimes • Best case runtime T best ( n ) ∈ O( n log n ) cn cn • Worst case runtime T worst ( n ) ∈ O( n 2 ) cn 1 cn cn 9 10 log 10 n 10 log 10/9 n • Worse than mergesort? Why is it called cn cn cn cn cn 1 9 9 81 100 100 100 100 quicksort then? … … • Its average runtime T avg ( n ) ∈ O( n log n ) … O ( n ) leaves Θ (1) O ( n ) leaves • Better even, the expected runtime of Θ (1) randomized quicksort is O( n log n ) Θ ( n log n ) cn log 10 n ≤ T ( n ) ≤ cn log 10/9 n + Ο ( n ) 2/17/09 CS 5633 Analysis of Algorithms 33 2/17/09 CS 5633 Analysis of Algorithms 34 Average Runtime Average Runtime The average runtime T avg ( n ) for Quicksort is • What kind of inputs are there? the average runtime over all possible inputs • Do [1,2,…, n ] and [5,6,…, n +5] cause of length n. different runtimes of Quicksort? • No. Therefore only consider all • What kind of inputs are there? permutations of [1,2,…, n ] . • How many inputs are there? • How many inputs are there? • There are n ! different permutations of [1,2,…, n ] 2/17/09 CS 5633 Analysis of Algorithms 35 2/17/09 CS 5633 Analysis of Algorithms 36 9