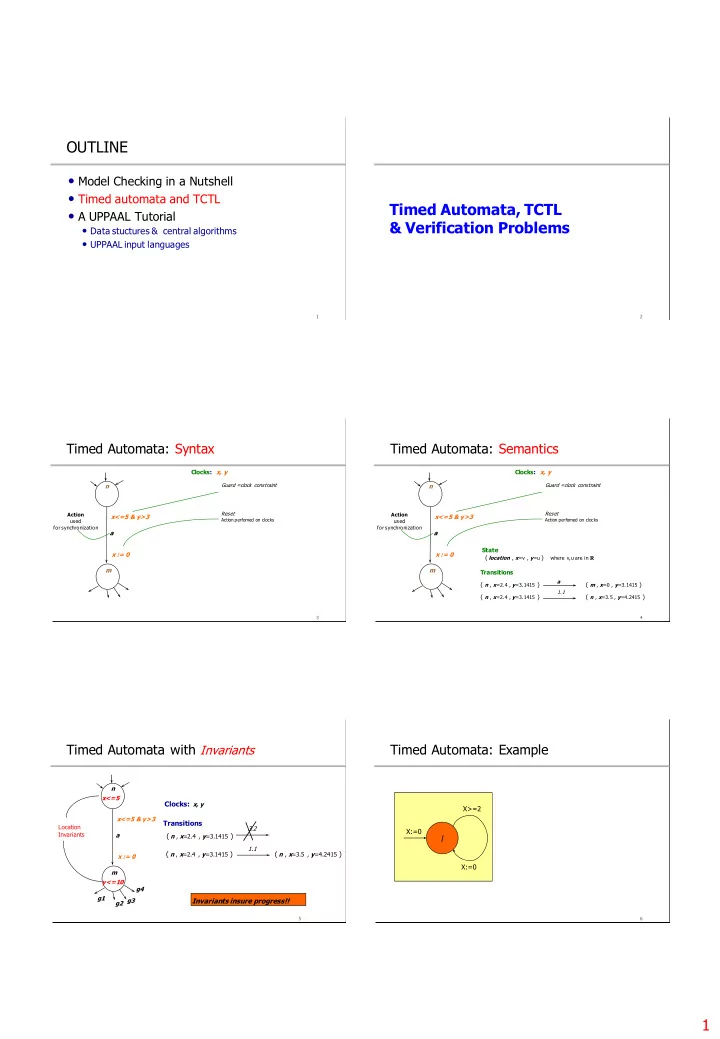

OUTLINE • Model Checking in a Nutshell • Timed automata and TCTL Timed Automata, TCTL • A UPPAAL Tutorial & Verification Problems • Data stuctures & central algorithms • UPPAAL input languages 1 2 Timed Automata: Syntax Timed Automata: Semantics Clocks: x, y Clocks: x, y n Guard =clock constraint n Guard =clock constraint Reset Reset Action Action x<=5 & y>3 x<=5 & y>3 Action perfomed on clocks Action perfomed on clocks used used for synchronization for synchronization a a State x := 0 x := 0 ( location , x =v , y =u ) where v,u are in R m m Transitions a ( n , x =2.4 , y =3.1415 ) ( m , x =0 , y =3.1415 ) 1.1 ( n , x =2.4 , y =3.1415 ) ( n , x =3.5 , y =4.2415 ) 3 4 Timed Automata with Invariants Timed Automata: Example n x<=5 Clocks: x, y X>=2 x<=5 & y>3 Transitions Location 3.2 X:=0 Invariants a ( n , x =2.4 , y =3.1415 ) l 1.1 ( n , x =2.4 , y =3.1415 ) ( n , x =3.5 , y =4.2415 ) x := 0 X:=0 m y<=10 g4 g1 g2 g3 Invariants insure progress!! 5 6 1
Timed Automata: Example Timed Automata: Example X>=2 2<=x<=3 X:=0 X:=0 l l X:=0 X:=0 7 8 Timed Automata: Example X>=2 Timed Automata X:=0 = l Finite Automata + Clock Constraints + Clock resets X <=3 X:=0 9 10 Semantics (definition) Clock Constraints clock valuations : R V ( C ) v : C 0 state : g ::= x n | g & g ( l , v ) where l L and v V ( C ) action transition a where ( l , v ) ( l ' , v ' ) iff g a r l’ l x is a clock variable g ( v ) and v ' v [ r ] and Inv ( l ' )( v ' ) {<, >, ≤, ≥} n is a natural number delay Transition d ( l , v ) ( l , v d ) iff Inv ( l )( v d ' ) whenever d ' d R 0 11 12 2
Modeling Concurrency CCS Parallel Composition (implemented in UPPAAL) Products of automata g a x:=0 g a x:=0 if m m’ then CCS Parallel composition (m,n) (m’,n) • implemented in UPPAAL g a x:=0 g a x:=0 if n n’ then (m,n) (m,n’) g c! x:=0 g&g’ x:=0 if m m’ then y:=0 (m,n) (m’,n’) g’ c? y:=0 and n’ n where a is an action c! or c? or , and c is a channel name 13 14 The UPPAAL Model = Networks of Timed Automata + Integer Variables +…. m1 l1 x>=2 y<=4 …………. Two-way synchronization i==3 on complementary actions. Verification Problems C! C? x := 0 Closed Systems! i:=i+4 l2 m2 Example transitions ( l1 , m1 ,………, x=2, y=3.5, i=3,…..) ( l2,m2 ,……..,x=0, y=3.5, i=7,…..) 15 16 Location Reachability (def.) (Timed) Language Inclusion, L(A) L(B) (a 0 , t 0 ) (a 1 , t 1 ) ... ... (a n , t n ) L(A) n is reachable from m if there is a sequence of transitions: If * ( m , u ) ( n , v ) ”A can perform a 0 at t 0 , a 1 at t 1 ... ... a n at t n ” t 0 a 0 (l 0 , u 0 ) (l 0 , u 0 +t 0 ) (l 1 , u 1 ) ... ... 17 18 3
Verification Problems Timed Language Equivalence & Inclusion • 1-clock, finite traces, decidable [ Ouaknine & Worrell 04] • 1-clock, infinite traces & Buchi-conditions, undecidable [Abdulla et al 05] Timed CTL = CTL + clock constraints Universality Untimed Language Inclusion Note that the semantics of TA defines a transition system (Un)Timed (Bi)simulation where each state has a Computation Tree Reachability Analysis/Emptiness Optimal Reachability (synthesis problem) • If a location is reachable, what is the minimal delay before reaching the location? 19 20 Computation Tree Logic, CTL Liveness: p - -> q ”p leads to q” Clarke & Emerson 1980 Syntax AG (p imply AF q) :: = P | | | EX | E[ U ] | A[ U ] where P AP (atomic propositions) Derived Operators p p AG p EG p EF p AF p q q q p p q q q 21 22 Timed CTL (a simplified version) Timed CTL (a simplified version) Syntax Syntax :: = p | | | EX | E[ U ] | A[ U ] :: = p | | | EX | E[ U ] | A[ U ] where p AP (atomic propositions) or Clock constraint where p AP (atomic propositions) or Clock constraint Derived Operators AG p EG p EF p AF p p p A[] P in UPPAAL E[] P in UPPAAL E<> P in UPPAAL A<> P in UPPAAL 23 24 4
Derived Operators (cont.) Bounded Liveness [TACAS 98] AG (p imply AF q) Verify : ”whenver p is true, q should be true within 10 sec X:=0 X:=0 X:=0 p X:=0 X:=0 X:=0 P - - > ( q and x<10 ) p p p Use extra clock x q Add x:=0 on all edges q q leading to P q q q q p - -> q in UPPAAL 25 26 Bounded Liveness/Responsiveness Bounded Liveness/Responsiveness (reachability analysis, more efficient?) (reachability analysis, more efficient?) [TACAS 98] [TACAS 98] This is not really correct; ” not Pb ” should be added as guard Verify : ”whenver p is true, Verify : ”whenver p is true, Pb := tt Pb := tt Pb := tt Pb := tt q should be true within 10 sec q should be true within 10 sec X:=0 X:=0 X:=0 X:=0 Pb := tt Pb := tt Pb := tt Pb := tt Pb := tt Pb := tt X:=0 Pb := tt X:=0 Pb := tt X:=0 X:=0 AG ((P b and x>10) imply q) X:=0 AG ((P b and x>10) imply q) X:=0 p X:=0 p X:=0 p p Use extra clock x and boolean P b Use extra clock x and boolean P b Add P b := tt and x:=0 on all edges Add P b := tt and x:=0 on all edges leading to location P leading to location P q q Pb:=ff should be On all eadges leaving q 27 28 Problem with Zenoness/Time-stop EXAMPLE We want to specify ”whenever P is true, y<=5 y<=5 Q should be true within 10 time units p y<=5 p y<=5 29 30 5
EXAMPLE EXAMPLE We want to specify ”whenever P is true, We want to specify ”whenever P is true, y<=5 y<=5 Q should be true within 10 time units Q should be true within 10 time units y<=5 p y<=5 p AG ((P b and x>10) imply Q) AG ((P b and x>10) imply q) P b :=true P b :=true x:=0 x:=0 is satisfied !!! 31 32 Solution with UPPAAL Check Zeno-freeness by an extra observer System || ZenoCheck REACHABILITY ANALYSIS A using Regions X<=1 Check (yes means ”no zeno loops”) X=1 B ZenoCheck.A - - > ZenoCheck.B x:=0 ZenoCheck Committed location! 33 34 Infinite State Space! Region: From infinite to finite Symbolic state (region ) Concrete State (n, ) (n, x=2.2, y=1.5 ) ∞ y y 2 2 1 1 x x 1 2 3 However , the reachability problem is decidable Alur&Dill 1991 1 2 3 An equivalence class (i.e. a region ) There are only finite many such!! 35 36 6
Region equivalence (Intuition) Region equivalence (Intuition) y y 2 2 u v iff (l,u) and (l,v) may reach u v iff (l,u) and (l,v) may reach the same set of eqivalence classes the same set of eqivalence classes d 1 1 1 2 3 x 1 2 3 x u v u v 37 38 Region equivalence [Alur and Dill 1990] Region equivalence (Intuition) u,v are clock assignments y u v iff • For all clocks x, either (1) u(x)>Cx and v(x)>Cx 2 u v iff (l,u) and (l,v) may reach or (2) u(x) = v(x) the same set of eqivalence classes • For all clocks x, if u(x)<=Cx, d 1 d’ {u(x)}=0 iff {v(x)}=0 • For all clocks x, y, if u(x)<=Cx and u(y)<=Cy {u(x)}<= {u(y)} iff {v(x)}<= {v(y)} 1 2 3 x u v 39 40 Region Graph Finite-State Transition System!! Region equivalence (alternatively) ) ... y y (n, (n, ) u v iff u and v satisfy exactly x:=0 the same set of constraints in 2 2 the form of ... xi ~ m and xi-xj ~ n (m, ) (m, ) 1 1 where ~ is in {<,>, , } and m,n < MAX ... 1 2 3 x 1 2 3 x This is not quite correct; OBS: there are only we need to consider the MAX u v (m, [u]) (n, [v]) if (m, u) (n,v) Finite many regions more carefully 41 42 7
Region graph of Theorem a simple timed automata u v implies X>=2 • u(x:=0) v(x:=0) • u+n v+n for all natural number n • for all d<1: u+d v+d’ for some d’<1 X:=0 l X:=0 ”Region equivalence’ is preserved by ”addition” and reset. (also preserved by ”subtraction” if clock values are ”bounded”) 43 44 CS AG CS 1 2 Fischers again Problems with Region Construction X<1 X:=0 X>1 V := 1 V=1 A1 B1 CS1 Y>1 Y<1 Y:=0 Untimed case V := 2 V=2 A2 B2 CS2 Too many ’regions’ Timed case • Sensitive to the maximal constants Partial A1,A2,v=1 • e.g. x>1,000,000, y>1,000,000 as guards in TA Region Graph A1,A2,v=1 A1,A2,v=1 A1,A2,v=1 A1,A2,v=1 x=y=0 0 <x=y <1 x=y=1 1 <x,y The number of regions is highly exponential in the A1,B2,v=2 number of clocks and the maximal constants. A1,B2,v=2 A1,B2,v=2 A1,B2,v=2 A1,B2,v=2 0 <x<1 0 <y < x<1 0 <y < x=1 0 <y<1 y=0 1 <x A1,CS2,v=2 A1,B2,v=2 A1,B2,v=2 1 <x,y y=1 B1,CS2,v=1 1 <x A1,CS2,v=2 1 <x,y CS1,CS2,v=1 No further behaviour possible!! 45 46 Zones: From infinite to finite Symbolic state (zone ) State (n, ) 1 x 4,1 y 3 (n, x=3.2, y=2.5 ) REACHABILITY ANALYSIS Zone: using ZONES conjunction of y y x-y~n, x~n ∞ x x 47 48 8
Recommend
More recommend