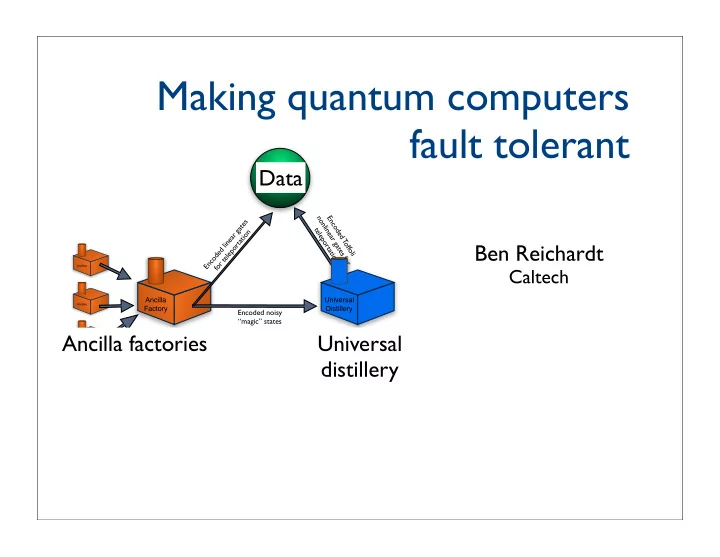

Making quantum computers fault tolerant Data Quantum data nonlinear gates for Encoded Toffoli Encoded linear gates teleportation for teleportation Ben Reichardt Ancillas Caltech Ancilla Universal Ancillas Factory Distillery Encoded noisy “magic” states Ancilla factories Universal Ancillas distillery •
Motivations for quantum information processing • Quantum computing (QC) • Simulation & modeling • • for quantum devices, Extended Church-Turing Thesis: • Anything physically efficiently chemistry, computable can be computed • materials (high-T superconductors, efficiently on my laptop new states of matter?) • QC: Extended Church-Turing Thesis • Quantum sensing is false; there are exponentially-faster • algorithms (for interesting problems) Precise measurement and by using quantum mechanics lithography • Atomic clocks • Cryptography • Basic science • • Breaks RSA public-key cryptosystem Investigate measurement/ • decoherence, quantum/classical Gives unconditionally secure key boundary distribution • Test qu. mechanics on new scales (but no free lunch…)
Quantum information � � α 0 = α 0 | 0 � + α 1 | 1 � 0 1 α 1 • “Qubit”: ( α x ) x ∈ { 0 , 1 } n | α 0 | 2 + | α 1 | 2 = 1 • State of n qubits = unit vector in C 2 n
Quantum information � � α 0 = α 0 | 0 � + α 1 | 1 � 0 1 α 1 • “Qubit”: ( α x ) x ∈ { 0 , 1 } n | α 0 | 2 + | α 1 | 2 = 1 • State of n qubits = unit vector in C 2 n ( α ′ x ) x ∈ { 0 , 1 } n • Computation by local gates, rotate the state vector • Observing/measuring system collapses it to a single classical bitstring x • No exponential parallelism • Have to “finesse” the quantum system to output the classical information you want
Classical information processing l 1 norm 1 • Classical state is a vector of probabilities: � 1 { p x } x ∈ { 0 , 1 } n p x = 1 p x ≥ 0 0 x • Valid operations are stochastic maps l 2 norm 1 Quantum information processing 1 -1 • Quantum state is also a vector 1 -1 0 | α x | 2 = 1 � { α x } x ∈ { 0 , 1 } n • Valid operations are rotations (unitaries) x 1 -1 The universe is quantum mechanical but it looks classical because of noise…
Quantum algorithms Today: Game tree New algorithmic Grover search evaluation approach based Search & Simulation on span programs random walk ...of dynamics of physical quantum systems Element distinctness Approx. Jones polynomial Approx. Jones polynomial Graph traversal CS+Physics Discrete log Factoring Fourier sampling & CS Hidden subgroup Polynomial Abelian, some nonabelian HSPs E x Pell's equation p o Graph n s p e isomorphism??? e n e t i d a u l p s
Quantum computing in 2008 • Ion traps • Superconducting qubits • can trap and cool 16-18 qubits • 2 qubit local interactions • can entangle 6-8 qubits in a trap becoming routine • nonlocal movement • microfabrication of trap arrays on chips, dealing & interactions now possible with increased noise [SHOMSM'05] • • in next 2-3 years may be able to compute with noise levels seem promising… 40-60 qubits • challenges: controlling thousands of traps with • Other technologies: dozens of detection channels and lasers along • the surface of the chip… Photonic qubits, quantum dots…
• Scaling these systems is a major engineering challenge • But the basic technologies have been proven, there are intermediate rewards • And there are no known fundamental difficulties, except… Common obstacle is noise! • Physically reasonable noise rates are ~1% error per gate, or maybe 0.1% ∴ Only 100 operations before an error can occur and propagate through the system • Factoring a 2048-bit number uses K-bit number: • 6 x 10 11 gates on versus e K ⅓ classically 72 K 3 gates • 10,000 qubits 5 K qubits • Need error 1/10 12 per gate �
Noise is fundamental problem for quantum computers: entangled systems are fragile dead cat • Schr ö dinger’s cat: � 1 2 , 1 � i.e. √ √ 2 1 √ 2 ( | live cat � + | dead cat � ) live cat • “Both dead and alive,” in superposition; but collapses to one or the other when observed • A single stray photon can collapse it — and also analogous states in a quantum computer • Physically reasonable noise rates are ~1% error per gate, or perhaps 0.1%
How to deal with noise? 1. Engineering • Not enough— noise is fundamental in quantum systems 2. Fault tolerance [Von Neumann ’56] • Enough to engineer the noise rate beneath a constant threshold, • Then effective noise rate can be decreased arbitrarily (and efficiently) using error- correcting codes
Classical fault tolerance [Von Neumann ‘56] , 0 Perfect op’s: Make fault-tolerant a circuit consisting of a universal 1 , set of operations, some faulty: Faulty op’s: AND, NOT 0 0 L = 0 0 0 1 1 0 0 m m n n o o o o d d i i n n 0 0 t 1 t a a a a t t r r u u 0 m m 1 r r e e 1 1 p 1 p 0 1 1 L = 1 Encoding Transversal Error correction gate application 0 1 fraction of 1’s
What’s different quantumly? • Quantum problems: • Quantum states are continuous, not discrete—need to protect against continuous errors • No-cloning theorem: Can’t copy a quantum state , so no | ψ � �→ | ψ � | ψ � immediate analog of the repetition code 0 �→ 0 n , 1 �→ 1 n • But quantum ECCs do exist! [Shor ’95] 1 0
Operational def. of QECC • Quantum problems: • Quantum states are continuous, not discrete—need to protect against continuous errors • No-cloning theorem: Can’t copy a quantum state , so no | ψ � �→ | ψ � | ψ � immediate analog of the repetition code 0 �→ 0 n , 1 �→ 1 n • But quantum ECCs do exist! [Shor ’95] Operationally, E ( | ψ � ) | ψ � encode ancilla qubits w/ encoded data data qubits error information append ancilla, copy ➋ errors inf. into it ➊ noise undo errors on encoded data E ( | ψ � ) N ⊗ m � � E ( | ψ � ) recover encoded data
Quantum error-correcting codes exist • Although quantum states are continuous, correcting a discrete set of errors (bit and phase flips) suffices • Based on classical linear ECCs: QECC comes from two linear ECCs (one for bit flips, one for phase flips) 1 bit flip error ( α β ) �→ ( β α ) 0 phase flip error ( α β ) �→ ( α − β )
Quantum error-correcting codes exist • Although quantum states are continuous, correcting a discrete set of errors (bit and phase flips) suffices • Based on classical linear ECCs: QECC comes from two linear ECCs (one for bit flips, one for phase flips) • How can we use these codes? • Need operations as well as memory • Error recovery must be resilient to faults during recovery • How to encode into them in the first place?? (qu problem) E ( | ψ � ) | ψ � encode ancilla qubits w/ encoded data data qubits error information append ancilla, copy ➋ errors inf. into it ➊ noise undo errors on encoded data E ( | ψ � ) N ⊗ m � � E ( | ψ � ) recover encoded data
Fault-tolerance intuition • Compile ideal circuit into “fault- cp 2 p Prob. diagram tolerant” (noise-resistant) version, fails to commute starting with small QECC: Threshold for Gate improvement: 1 /c �− → 1 level Encoded Error 2 levels gate correction 3 levels 4 levels p (0 , 0) Physical error rate p • Concatenate (i.e., repeat) for arbitrarily perfect perfect decoding decoding improved reliability (so arb ly long calcs), if starting below a constant noise threshold • Problem: Noise model at encoded level is perfect gate not the same as the physical noise model!
Abridged History of Quantum Fault Tolerance • 1996-97: First fault-tolerance results: QECCs, threshold proofs Shor, Steane, Calderbank, Aharonov, Ben-Or, Kitaev, Knill, Laflamme, Zurek, … • Proved existence of some positive tolerable noise rate using concatenated qu. codes of distance ≥ 5 • No explicit lower bounds on tolerable noise rate, but estimates were 10 -6 -10 -5 noise per gate • Moral: Fault tolerance makes quantum computers plausible in the real world "Dark Ages" -D. Gottesman
Abridged History of Quantum Fault Tolerance Estimates & Proofs simulations • 1997: Aharonov/Ben-Or, Kitaev: Prove • 2002: Steane: Correct bit flip errors all at positive tolerable noise rate for codes once, and then phase flip errors all at once of distance d ≥ 5 • based on simulations, estimates 3x10 -3 • 2005: R, Aliferis/Gottesman/Preskill: tolerable noise rate per gate First explicit numerical threshold lower bounds, threshold for distance-3 codes Simulations using distance-3 codes • Basic estimates: • Optimized estimates: • 2D locality constraint • • • Szkopek et al ‘04 Aharonov & Ben-Or ‘97 Zalka ‘97 • • • Svore-Terhal-DiVincenzo ‘05 Gottesman ‘97 R ‘04 • • Knill-Laflamme-Zurek ‘98 Svore-Cross- Chuang-Aho ‘05 • Preskill ‘98
Recommend
More recommend