Locally identifying colorings of graphs Aline Parreau Joint work - PowerPoint PPT Presentation

Locally identifying colorings of graphs Aline Parreau Joint work with: Louis Esperet, Sylvain Gravier, Micka¨ el Montassier, Pascal Ochem and: Florent Foucaud, Iiro Honkala, Tero Laihonen, Guillem Perarnau Bordeaux Workshop on Identifying Codes November 21-25, 2011 1/13

Identification with colors ? Identifying coloring of a graph G : • c : V → N • c ( N [ x ]) � = c ( N [ y ]) for any vertices x � = y • χ id ( G ): minimum number of colors needed to identify G 1 2 1 2 3 2 2/13

Identification with colors ? Identifying coloring of a graph G : • c : V → N • c ( N [ x ]) � = c ( N [ y ]) for any vertices x � = y • χ id ( G ): minimum number of colors needed to identify G { 1 , 2 } { 1 , 2 , 3 } { 1 , 2 } 1 2 1 2 3 2 { 1 , 2 , 3 } { 2 , 3 } { 1 , 2 , 3 } 2/13

Identification with colors ? Identifying coloring of a graph G : • c : V → N • c ( N [ x ]) � = c ( N [ y ]) for any vertices x � = y • χ id ( G ): minimum number of colors needed to identify G { 1 , 2 } { 1 , 2 , 3 , 4 } { 2 , 4 } 1 2 4 2 3 2 { 1 , 2 , 3 } { 2 , 3 } { 2 , 3 , 4 } 2/13

Identification with colors ? Identifying coloring of a graph G : • c : V → N • c ( N [ x ]) � = c ( N [ y ]) for any vertices x � = y • χ id ( G ): minimum number of colors needed to identify G Few remarks: • only exists for twin-free graphs (like id-codes) • χ id ( G ) ≤ γ ID ( G ) + 1 1 2 3 ⇒ 4 4 4 2/13

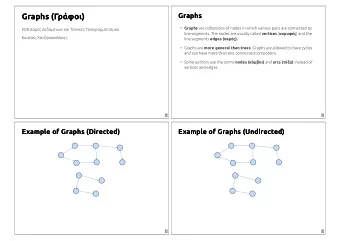
Global to local colorings Identifying coloring of a graph G = ( V , E ): • c : V → N ; • For any x � = y in V , c ( N [ x ]) � = c ( N [ y ]); • χ id ( G ): minimum number of colors needed to identify G ; Locally identifying coloring (lid-coloring) of a graph G = ( V , E ): • c : V → N , c ( x ) � = c ( y ) for xy ∈ E ; • For any xy ∈ E , c ( N [ x ]) � = c ( N [ y ]), if possible ; • χ lid ( G ): min. number of colors needed to locally identify G . 3/13

Global to local colorings Identifying coloring of a graph G = ( V , E ): • c : V → N ; • For any x � = y in V , c ( N [ x ]) � = c ( N [ y ]); • χ id ( G ): minimum number of colors needed to identify G ; Locally identifying coloring (lid-coloring) of a graph G = ( V , E ): • c : V → N , c ( x ) � = c ( y ) for xy ∈ E ; • For any xy ∈ E , c ( N [ x ]) � = c ( N [ y ]), if possible ; • χ lid ( G ): min. number of colors needed to locally identify G . Why? • Always exists. • Refinment of classic colorings: χ ( G ) ≤ χ lid ( G ) 3/13

An example Def: ∀ xy ∈ E , c ( x ) � = c ( y ) and c ( N [ x ]) � = c ( N [ y ]) 4/13

An example Def: ∀ xy ∈ E , c ( x ) � = c ( y ) and c ( N [ x ]) � = c ( N [ y ]) 4/13

An example Def: ∀ xy ∈ E , c ( x ) � = c ( y ) and c ( N [ x ]) � = c ( N [ y ]) 3 1 2 4 4 2 3 1 2 4 1 3 1 3 4 2 χ lid ( G ) ≤ 4 4/13

An example Def: ∀ xy ∈ E , c ( x ) � = c ( y ) and c ( N [ x ]) � = c ( N [ y ]) 1 1 χ lid ( G ) ? = 4 4/13

An example Def: ∀ xy ∈ E , c ( x ) � = c ( y ) and c ( N [ x ]) � = c ( N [ y ]) 1 3 2 1 χ lid ( G ) ? = 4 4/13

An example Def: ∀ xy ∈ E , c ( x ) � = c ( y ) and c ( N [ x ]) � = c ( N [ y ]) 1 3 2 1 χ lid ( G ) = 4 but χ ( G ) = 3 4/13

An example Def: ∀ xy ∈ E , c ( x ) � = c ( y ) and c ( N [ x ]) � = c ( N [ y ]) 1 3 2 1 χ lid ( G ) = 4 but χ ( G ) = 3 For each k , there exists graph G k s.t χ ( G k ) = 3 and χ lid ( G k ) = k No upper bound with χ ! 4/13

Upper bound on a graph with n vertices ? Classic colorings: χ ( G ) = n ⇔ G = K n Lid-colorings: for which graphs χ lid ( G ) = n ? 5/13

Upper bound on a graph with n vertices ? Classic colorings: χ ( G ) = n ⇔ G = K n Lid-colorings: for which graphs χ lid ( G ) = n ? • K n • P k − 1 : 2 k 1 2 3 4 5 6 Extremal graph for identifying codes ! 5/13

Upper bound on a graph with n vertices ? Classic colorings: χ ( G ) = n ⇔ G = K n Lid-colorings: for which graphs χ lid ( G ) = n ? • K n • P k − 1 : 2 k 1 2 3 4 5 6 Extremal graph for identifying codes ! • ... ? Open question Caracterize graphs G such that χ lid ( G ) = n . 5/13

Maximum degree Classic colorings: χ ( G ) ≤ ∆ + 1, tight Lid-colorings: • χ lid ( G ) ≤ χ ( G 3 ) ≤ ∆ 3 − ∆ 2 + ∆ + 1 • Graphs with χ lid ( G ) ≥ ∆ 2 − ∆ + 1 6/13

Maximum degree Classic colorings: χ ( G ) ≤ ∆ + 1, tight Lid-colorings: • χ lid ( G ) ≤ χ ( G 3 ) ≤ ∆ 3 − ∆ 2 + ∆ + 1 • Graphs with χ lid ( G ) ≥ ∆ 2 − ∆ + 1 6/13

Maximum degree Classic colorings: χ ( G ) ≤ ∆ + 1, tight Lid-colorings: • χ lid ( G ) ≤ χ ( G 3 ) ≤ ∆ 3 − ∆ 2 + ∆ + 1 • Graphs with χ lid ( G ) ≥ ∆ 2 − ∆ + 1 Theorem (Foucaud,Honkala,Laihonen,P.,Perarnau, 2011 + ) For any graph G with ∆ ≥ 3: χ lid ( G ) ≤ 2∆ 2 − 3∆ + 3 Open question Do we always have χ lid ( G ) ≤ ∆ 2 + O (∆) ? 6/13

Bipartite graphs: the paths With 4 colors : 7/13

Bipartite graphs: the paths With 4 colors : 1 2 3 4 1 2 3 4 7/13

Bipartite graphs: the paths With 4 colors : 1 2 3 4 1 2 3 4 1 , 2 1 , 2 , 3 2 , 3 , 4 1 , 3 , 4 1 , 2 , 4 1 , 2 , 3 2 , 3 , 4 3 , 4 So: χ lid ( P k ) ≤ 4 7/13

Bipartite graphs: the paths With 4 colors : 1 2 3 4 1 2 3 4 1 , 2 1 , 2 , 3 2 , 3 , 4 1 , 3 , 4 1 , 2 , 4 1 , 2 , 3 2 , 3 , 4 3 , 4 So: χ lid ( P k ) ≤ 4 Is it possible with 3 colors ? 7/13

Bipartite graphs: the paths With 4 colors : 1 2 3 4 1 2 3 4 1 , 2 1 , 2 , 3 2 , 3 , 4 1 , 3 , 4 1 , 2 , 4 1 , 2 , 3 2 , 3 , 4 3 , 4 So: χ lid ( P k ) ≤ 4 Is it possible with 3 colors ? 1 2 1 , 2 7/13

Bipartite graphs: the paths With 4 colors : 1 2 3 4 1 2 3 4 1 , 2 1 , 2 , 3 2 , 3 , 4 1 , 3 , 4 1 , 2 , 4 1 , 2 , 3 2 , 3 , 4 3 , 4 So: χ lid ( P k ) ≤ 4 Is it possible with 3 colors ? 1 2 3 1 , 2 1 , 2 , 3 7/13

Bipartite graphs: the paths With 4 colors : 1 2 3 4 1 2 3 4 1 , 2 1 , 2 , 3 2 , 3 , 4 1 , 3 , 4 1 , 2 , 4 1 , 2 , 3 2 , 3 , 4 3 , 4 So: χ lid ( P k ) ≤ 4 Is it possible with 3 colors ? 1 2 3 2 1 , 2 1 , 2 , 3 2 , 3 7/13

Bipartite graphs: the paths With 4 colors : 1 2 3 4 1 2 3 4 1 , 2 1 , 2 , 3 2 , 3 , 4 1 , 3 , 4 1 , 2 , 4 1 , 2 , 3 2 , 3 , 4 3 , 4 So: χ lid ( P k ) ≤ 4 Is it possible with 3 colors ? 1 2 3 2 1 2 3 2 2 , 3 2 , 3 1 , 2 1 , 2 , 3 2 , 3 1 , 2 , 3 1 , 2 1 , 2 , 3 χ lid ( P k ) = 3 ⇔ k is odd ... χ lid is not heriditary ! 7/13

Bipartite graphs L 0 L 1 L 2 L 3 L 4 8/13

Bipartite graphs → L 0 1 1 , 2 → L 1 2 1 , 2 , 3 → L 2 3 2 , 3 , 4 or 2 , 3 → L 3 4 1 , 3 , 4 or 3 , 4 → L 4 1 1 , 4 • 3 ≤ χ lid ( B ) ≤ 4 • To decide between 3 and 4 is NP-complete (reduction from 2-coloring of hypergraph) • Polynomial for trees, grids and hypercubes ( χ lid = 3), regular bipartite graphs... 8/13

Perfect Graphs Perfect Line of bipartite Permutation Cograph Chordal Bipartite Split Interval k -trees Trees 9/13

Perfect Graphs Perfect Line of bipartite Permutation Cograph Chordal Bipartite Bipartite ≤ 4 = 2 χ Split Interval k -trees ≤ 4 = 2 χ Trees Trees 9/13

Perfect Graphs Not bounded by χ Perfect Perfect Line of bipartite Permutation Cograph Cograph Chordal Chordal ? ≤ 2 χ Bipartite Bipartite ≤ 4 = 2 χ Split Split Interval Interval k -trees k -trees ≤ 2 χ ≤ 2 χ ≤ 2 χ ≤ 4 = 2 χ Trees Trees Open question Do we have χ lid ( G ) ≤ 2 χ ( G ) for a chordal graph G ? 9/13

Planar Graphs Planar graphs: • Worse example : 8 colors, • Really large (1000 ?) bound by Gonzcales and Pinlou P 3 8 10/13

Planar Graphs Planar graphs: • Worse example : 8 colors, • Really large (1000 ?) bound by Gonzcales and Pinlou • With large girth (36) bounded by 5 P 3 8 10/13

Planar Graphs Planar graphs: • Worse example : 8 colors, • Really large (1000 ?) bound by Gonzcales and Pinlou • With large girth (36) bounded by 5 P 3 8 10/13

Planar Graphs Planar graphs: • Worse example : 8 colors, • Really large (1000 ?) bound by Gonzcales and Pinlou • With large girth (36) bounded by 5 P 3 8 Outerplanar graphs: • General bound: 20 colors, • Max outerplanar graphs: ≤ 6 colors, • Without triangles: ≤ 8 colors, P 2 • Examples with at most 6 colors 6 Open question Do we have χ lid ( G ) ≤ 8 for planar graphs and χ lid ( G ) ≤ 6 for outer- planar graphs ? 10/13

A remark • For some subclasses of perfect graphs : χ lid ( G ) ≤ 2 ω ( G ) = 2 χ ( G ) • For planar graphs, worse example : χ lid ( G ) ≤ 8 = 2 χ ( G ) • For outerplanar graphs, worse example : χ lid ( G ) ≤ 6 = 2 χ ( G ) • ... Open question For which graphs do we have χ lid ( G ) ≤ 2 χ ( G ) ? 11/13

Another remark • χ lid ( G ) = 2 ⇔ G = K 2 • χ lid ( G ) = 3 ⇒ G = K 3 or G is bipartite • χ lid ( G ) = 3 and χ ( G ) = 3 ⇔ G = K 3 Open question Caracterize graphs G such that χ lid ( G ) = χ ( G ). Are they only the complete graphs ? 12/13